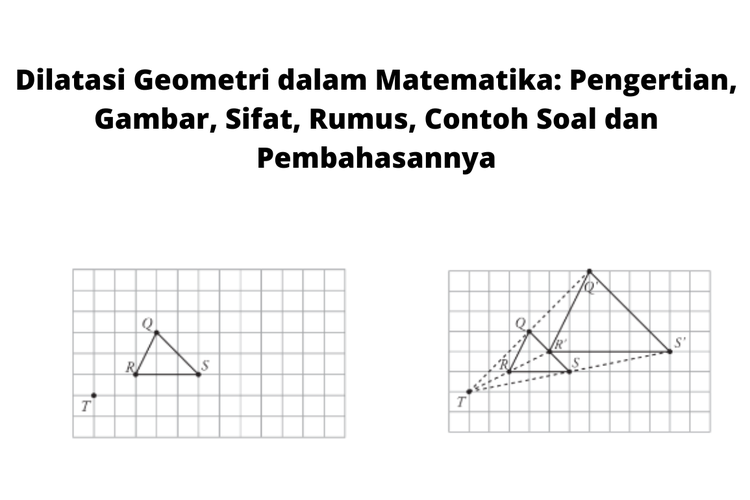
Pengertian dan Rumus Dilatasi dalam Matematika yang Wajib Dipahami
Dilatasi adalah salah satu konsep penting dalam matematika, khususnya dalam transformasi geometri. Dalam bahasa sederhana, dilatasi merujuk pada proses mengubah ukuran suatu objek tanpa mengubah bentuknya. Bayangkan memperbesar atau memperkecil sebuah foto; itulah inti dari konsep ini. Meskipun terdengar sederhana, pemahaman tentang dilatasi sangat penting tidak hanya dalam matematika, tetapi juga dalam berbagai bidang seperti desain grafis, arsitektur, dan seni.
Dilatasi dapat diterapkan dalam berbagai situasi, mulai dari pembuatan ilusi perspektif hingga pengaturan skala dalam proyek visual. Pemahaman dasar tentang rumus dilatasi serta bagaimana cara menggunakannya akan membantu Anda menguasai konsep ini dengan lebih baik. Artikel ini akan menjelaskan secara rinci pengertian dilatasi, rumus-rumus yang digunakan, contoh soal, dan aplikasinya dalam kehidupan sehari-hari.
Secara teknis, dilatasi melibatkan dua komponen utama: faktor skala (scale factor) dan titik pusat dilatasi. Faktor skala menentukan seberapa besar objek akan diperbesar atau diperkecil, sedangkan titik pusat menjadi acuan untuk perubahan ukuran tersebut. Misalnya, jika kita memiliki titik A(2, 3) dan melakukan dilatasi dengan faktor skala 2 dan titik pusat di titik asal (0, 0), maka titik A akan berpindah ke titik A'(4, 6). Perubahan ini terjadi karena koordinat x dan y dikalikan dengan faktor skala.
Selain itu, faktor skala negatif juga bisa digunakan dalam dilatasi. Jika nilai k negatif, selain perubahan ukuran, terjadi pula refleksi (pencerminan) terhadap titik pusat. Contohnya, jika k = -1, titik A(2, 3) akan berpindah ke titik A'(-2, -3). Hal ini menunjukkan bahwa posisi titik bayangan berlawanan arah terhadap titik pusat.
Untuk memahami lebih jauh, mari kita lihat bagaimana rumus dilatasi bekerja dalam berbagai situasi. Rumus ini bergantung pada lokasi titik pusat dan faktor skala yang digunakan. Jika titik pusat berada di titik asal (0, 0), maka rumusnya cukup sederhana. Namun, jika titik pusat berada di titik lain, seperti (a, b), maka rumusnya sedikit lebih kompleks. Dengan memahami rumus ini, Anda akan mampu menghitung koordinat bayangan dari setiap objek yang didilatasi.
Pengertian Dasar Dilatasi dalam Matematika
Dilatasi adalah transformasi geometri yang mengubah ukuran suatu objek tanpa mengubah bentuknya. Proses ini melibatkan dua elemen utama: faktor skala dan titik pusat. Faktor skala menentukan seberapa besar objek akan diperbesar atau diperkecil, sedangkan titik pusat menjadi acuan untuk perubahan ukuran tersebut.
Contoh sederhana dari dilatasi adalah ketika Anda memperbesar gambar menggunakan aplikasi edit foto. Gambar tersebut tetap memiliki bentuk yang sama, tetapi ukurannya berubah. Dalam konteks matematika, hal ini serupa dengan mengubah koordinat titik-titik yang membentuk suatu bangun. Misalnya, jika Anda memiliki titik A(2, 3) dan melakukan dilatasi dengan faktor skala 2 dan titik pusat di titik asal (0, 0), maka titik A akan berpindah ke titik A'(4, 6).
Pemahaman tentang dilatasi sangat penting dalam berbagai bidang. Dalam desain grafis, misalnya, dilatasi digunakan untuk menciptakan efek visual yang menarik. Dalam arsitektur, konsep ini digunakan untuk menggambar denah bangunan dengan skala yang sesuai. Bahkan dalam seni, dilatasi bisa digunakan untuk menciptakan karya yang menampilkan perubahan ukuran secara estetis.
Selain itu, dilatasi juga memiliki implikasi dalam matematika lanjutan, seperti dalam geometri analitis dan aljabar linear. Pemahaman dasar tentang konsep ini akan memudahkan Anda dalam mempelajari topik-topik yang lebih kompleks. Oleh karena itu, sangat penting untuk memahami pengertian dasar dilatasi sebelum melangkah ke rumus dan contoh soal.
Rumus Dasar Dilatasi dalam Matematika
Rumus dasar dilatasi sangat sederhana dan mudah dipahami. Jika Anda memiliki sebuah titik P(x, y) dan ingin melakukan dilatasi dengan pusat O(0, 0) dan faktor skala k, maka koordinat titik P’ (bayangan titik P) dapat dihitung menggunakan rumus berikut:
P'(kx, ky)
Artinya, koordinat x dan y dari titik P akan dikalikan dengan faktor skala k. Misalnya, jika titik P(2, 3) didilatasi dengan faktor skala 2, maka titik P’ akan berada di (4, 6). Jika faktor skala lebih besar dari 1, objek akan diperbesar. Sebaliknya, jika faktor skala antara 0 dan 1, objek akan diperkecil.
Namun, jika pusat dilatasi bukan di titik asal (0, 0), misalnya di titik A(a, b), maka rumusnya sedikit berbeda. Dalam kasus ini, rumus dilatasi menjadi:
P'(k(x – a) + a, k(y – b) + b)
Rumus ini menunjukkan bahwa kita perlu menghitung selisih antara koordinat titik P dengan koordinat titik pusat dilatasi, kemudian mengalikannya dengan faktor skala, dan menambahkan kembali koordinat titik pusat dilatasi. Misalnya, jika titik P(2, 3) didilatasi dengan pusat A(1, 1) dan faktor skala 2, maka:
- x’ = 2(2 – 1) + 1 = 21 + 1 = 3
- y’ = 2(3 – 1) + 1 = 22 + 1 = 5
Jadi, titik P’ akan berada di (3, 5).
Selain itu, faktor skala negatif juga bisa digunakan dalam dilatasi. Jika k < 0, selain terjadi perubahan ukuran, juga terjadi refleksi (pencerminan) terhadap titik pusat dilatasi. Contohnya, jika k = -1, maka titik P(2, 3) akan berpindah ke titik P’(-2, -3). Titik P’ tidak hanya berjarak yang sama dari titik O seperti titik P, tetapi juga berada di sisi yang berlawanan dari titik O.
Dengan memahami rumus dasar ini, Anda akan mampu menghitung koordinat bayangan dari setiap objek yang didilatasi. Ini merupakan langkah awal yang penting dalam menguasai konsep dilatasi dalam matematika.
Faktor Skala dalam Dilatasi
Faktor skala (k) adalah elemen krusial dalam dilatasi. Nilai k menentukan seberapa besar atau seberapa kecil objek akan berubah. Jika k > 1, maka objek akan diperbesar. Semakin besar nilai k, semakin besar pula perbesarannya. Misalnya, jika k = 2, maka objek akan diperbesar dua kali lipat dari ukuran aslinya.
Sebaliknya, jika 0 < k < 1, maka objek akan diperkecil. Semakin kecil nilai k (mendekati 0), semakin kecil pula pengecilannya. Misalnya, jika k = 0.5, maka objek akan diperkecil menjadi setengah dari ukuran aslinya. Jika k = 1, maka dilatasi tidak akan mengubah ukuran objek sama sekali (identitas).
Penting untuk memahami peran faktor skala ini agar dapat melakukan dilatasi dengan tepat. Dalam praktiknya, faktor skala bisa digunakan untuk mengatur ukuran objek sesuai kebutuhan. Misalnya, dalam desain grafis, Anda bisa menggunakan faktor skala untuk membuat ilusi perspektif atau menyesuaikan ukuran objek agar sesuai dengan tata letak gambar.
Selain itu, faktor skala negatif juga bisa digunakan dalam dilatasi. Jika k < 0, selain terjadi perubahan ukuran, juga terjadi refleksi (pencerminan) terhadap titik pusat dilatasi. Contohnya, jika k = -1, maka titik P(2, 3) akan berpindah ke titik P’(-2, -3). Titik P’ tidak hanya berjarak yang sama dari titik O seperti titik P, tetapi juga berada di sisi yang berlawanan dari titik O.
Dengan memahami peran faktor skala, Anda akan lebih mudah mengimplementasikan konsep dilatasi dalam berbagai situasi. Faktor skala tidak hanya menentukan ukuran objek, tetapi juga memengaruhi posisi dan orientasi objek setelah dilatasi.
Pusat Dilatasi dalam Transformasi Geometri
Pusat dilatasi adalah titik yang menjadi acuan dalam proses perubahan ukuran. Semua titik pada objek awal akan “bergerak” menjauhi atau mendekati titik pusat ini. Lokasi pusat dilatasi sangat penting karena akan mempengaruhi hasil akhir dari dilatasi. Jika pusat dilatasi berbeda, maka hasil dilatasi juga akan berbeda, meskipun faktor skala yang digunakan sama.
Pusat dilatasi bisa berada di dalam objek, di luar objek, atau bahkan di salah satu titik pada objek itu sendiri. Posisi relatif pusat dilatasi terhadap objek akan menentukan bagaimana objek tersebut berubah ukurannya. Misalnya, jika pusat dilatasi berada di tengah-tengah objek, maka objek akan diperbesar atau diperkecil secara merata dari pusat. Namun, jika pusat dilatasi berada di luar objek, maka objek akan terlihat seperti bergerak menjauhi atau mendekati pusat dilatasi tersebut.
Dalam desain grafis, pemilihan pusat dilatasi yang tepat dapat menghasilkan efek visual yang menarik. Misalnya, kita dapat membuat ilusi perspektif dengan menempatkan pusat dilatasi di kejauhan, sehingga objek-objek yang lebih dekat terlihat lebih besar daripada objek-objek yang lebih jauh. Dalam arsitektur, pusat dilatasi bisa digunakan untuk menggambar denah bangunan dengan skala yang sesuai.
Memahami pengaruh posisi pusat dilatasi sangat penting dalam mengaplikasikan dilatasi dalam berbagai konteks. Dengan memahami bagaimana pusat dilatasi memengaruhi hasil akhir, Anda akan lebih mudah mengontrol perubahan ukuran objek sesuai kebutuhan.
Contoh Soal Dilatasi dan Pembahasannya
Untuk memperdalam pemahaman Anda tentang dilatasi, mari kita bahas beberapa contoh soal beserta pembahasannya. Contoh 1: Titik A(3, 4) didilatasikan dengan pusat O(0, 0) dan faktor skala 2. Tentukan koordinat bayangan titik A.
Pembahasan:
Menggunakan rumus P'(kx, ky), kita dapatkan A'(2 * 3, 2 * 4) = A'(6, 8). Jadi, koordinat bayangan titik A adalah (6, 8).
Contoh 2: Segitiga ABC dengan koordinat A(1, 1), B(3, 1), dan C(1, 3) didilatasikan dengan pusat P(2, 2) dan faktor skala 0.5. Tentukan koordinat bayangan segitiga ABC.
Pembahasan:
Kita perlu menggunakan rumus P'(k(x – a) + a, k(y – b) + b) untuk setiap titik.
- A'(0.5(1 – 2) + 2, 0.5(1 – 2) + 2) = A'(1.5, 1.5)
- B'(0.5(3 – 2) + 2, 0.5(1 – 2) + 2) = B'(2.5, 1.5)
- C'(0.5(1 – 2) + 2, 0.5(3 – 2) + 2) = C'(1.5, 2.5)
Jadi, koordinat bayangan segitiga ABC adalah A'(1.5, 1.5), B'(2.5, 1.5), dan C'(1.5, 2.5).
Contoh 3: Titik (-12, 8) didilatasi pusat O [0,0] dan faktor skala -5/4. Koordinat bayangan titik L adalah...
Pembahasan:
P (x,y) [0,k] à P'(kx, ky)
P (-12,8) [0, -5/4] à P'(...)
- X' = -12. -5/4 = 15
- Y' = 8. -5/4 = -10
L' = (15, -10)
Contoh 4: Dari sebuah garis yang ditarik dari titik a(2, 1) hingga b(2, 3) dilakukan transformasi dilatasi terhadap titik j(1, 2) sebesar k = 2, hitunglah bayangan dari garis tersebut!
Pembahasan:
Garis a(2, 1) hingga b(2, 3) terhadap titik j(1, 2) sebesar k = 2.
Mencari nilai a':
- x’ = 2(2 – 1) + 1 = 21 + 1 = 3
- y’ = 2(1 – 2) + 2 = 2(-1) + 2 = 0
Mencari nilai b':
- x’ = 2(2 – 1) + 1 = 21 + 1 = 3
- y’ = 2(3 – 2) + 2 = 21 + 2 = 4
Jadi, bayangan garis tersebut digambarkan sebagai garis yang ditarik dari a'(3, 0) hingga b'(3, 4).
Contoh soal ini menunjukkan bagaimana rumus dilatasi diterapkan dalam kasus yang berbeda. Dengan berlatih lebih banyak soal, Anda akan semakin mahir dalam mengaplikasikan konsep dilatasi.
Aplikasi Praktis Dilatasi dalam Kehidupan Sehari-hari
Dilatasi tidak hanya relevan dalam dunia matematika, tetapi juga memiliki berbagai aplikasi praktis dalam kehidupan sehari-hari. Salah satu contoh paling umum adalah dalam desain grafis dan pengeditan foto. Ketika Anda memperbesar atau memperkecil gambar menggunakan software seperti Photoshop atau GIMP, Anda sedang menerapkan konsep dilatasi. Dalam kasus ini, faktor skala menentukan seberapa besar gambar akan berubah ukurannya, sementara titik pusat dilatasi menentukan di mana perubahan tersebut akan terjadi.
Di bidang arsitektur, dilatasi digunakan untuk membuat denah bangunan dengan skala yang sesuai. Misalnya, ketika seorang arsitek membuat model miniatur dari sebuah gedung, mereka menggunakan prinsip dilatasi untuk memperkecil ukuran bangunan asli sesuai dengan skala yang ditentukan. Dalam kasus ini, titik pusat dilatasi biasanya berada di tengah-tengah model, sehingga semua bagian bangunan diperkecil secara merata.
Dalam seni, dilatasi bisa digunakan untuk menciptakan karya yang menampilkan perubahan ukuran secara estetis. Misalnya, seniman bisa menggunakan prinsip ini untuk membuat lukisan yang menampilkan objek-objek dengan ukuran yang berbeda-beda, menciptakan ilusi kedalaman dan perspektif. Dalam konteks ini, faktor skala dan titik pusat dilatasi memengaruhi bagaimana objek-objek tersebut terlihat pada kanvas.
Selain itu, dilatasi juga digunakan dalam bidang teknik dan ilmu pengetahuan. Dalam pengambilan gambar medis, misalnya, konsep dilatasi digunakan untuk memperbesar gambar organ tubuh agar lebih mudah dianalisis. Dalam astronomi, ilmuwan menggunakan prinsip ini untuk memperbesar gambar bintang dan galaksi agar bisa dilihat dengan lebih jelas.
Dengan demikian, dilatasi tidak hanya menjadi konsep teoretis dalam matematika, tetapi juga memiliki peran penting dalam berbagai bidang nyata. Pemahaman tentang konsep ini akan membantu Anda mengaplikasikannya dalam berbagai situasi, baik dalam pekerjaan profesional maupun kegiatan sehari-hari.

0Komentar