Resultan gaya adalah salah satu konsep dasar dalam ilmu fisika yang sering muncul dalam berbagai situasi sehari-hari. Dari permainan tarik tambang hingga pengangkatan benda, semua melibatkan penjumlahan atau pengurangan gaya yang bekerja pada suatu objek. Memahami rumus resultan gaya tidak hanya membantu Anda menyelesaikan soal-soal fisika, tetapi juga meningkatkan pemahaman tentang bagaimana gaya bekerja di dunia nyata.
Dalam artikel ini, kita akan menjelajahi secara mendalam mengenai apa itu resultan gaya, bagaimana cara menghitungnya, serta penerapan praktisnya dalam kehidupan sehari-hari. Kami akan membahas tiga jenis utama resultan gaya, yaitu resultan gaya searah, berlawanan, dan tegak lurus, serta contoh soal yang mudah dipahami. Selain itu, kami juga akan memberikan informasi terkini tentang pentingnya memahami konsep ini dalam studi fisika dan aplikasinya dalam bidang teknik dan sains modern.
Pemahaman yang baik tentang resultan gaya sangat penting karena merupakan fondasi dari banyak prinsip fisika seperti hukum Newton, gerak, dan keseimbangan. Dengan mengetahui bagaimana gaya saling memengaruhi, Anda dapat lebih mudah memprediksi hasil dari berbagai situasi fisik yang kompleks. Mari mulai dengan pengertian dasar tentang resultan gaya.
Pengertian Resultan Gaya
Resultan gaya adalah jumlah total dari semua gaya yang bekerja pada suatu benda atau sistem. Karena gaya merupakan besaran vektor, maka resultan gaya harus diperhitungkan baik dari segi besar maupun arahnya. Dalam bahasa sederhana, resultan gaya bisa diartikan sebagai "gaya total" yang bekerja pada suatu objek. Jika dua atau lebih gaya bekerja pada benda yang sama, maka resultan gaya adalah jumlah atau selisih dari gaya-gaya tersebut, tergantung pada arahnya.
Contoh sederhana dari resultan gaya adalah saat kamu dan temanmu sedang bermain tarik tambang. Jika kamu menarik tambang dengan gaya 50 N dan temanmu hanya 40 N, maka resultan gaya akan menjadi 10 N ke arah kamu, sehingga kamu akan menang. Hal ini menunjukkan bahwa resultan gaya tidak hanya bergantung pada besar gaya, tetapi juga pada arahnya.
Secara matematis, resultan gaya dapat ditulis sebagai:
$$ F_R = F_1 + F_2 + F_3 + \dots + F_n $$
di mana $ F_R $ adalah resultan gaya, dan $ F_1, F_2, F_3, \dots, F_n $ adalah gaya-gaya yang bekerja pada sistem. Namun, jika gaya-gaya tersebut memiliki arah berbeda, maka penjumlahannya harus dilakukan dengan memperhatikan tanda positif dan negatif sesuai dengan arahnya.
Memahami konsep ini sangat penting dalam fisika karena resultan gaya digunakan untuk menentukan percepatan, keseimbangan, dan gerakan suatu benda. Dengan demikian, pemahaman yang baik tentang resultan gaya akan membantu Anda dalam memecahkan berbagai masalah fisika yang kompleks.
Jenis-Jenis Resultan Gaya
Berdasarkan arah dan besar gaya yang bekerja, resultan gaya dibagi menjadi tiga jenis utama: resultan gaya searah, resultan gaya berlawanan, dan resultan gaya tegak lurus. Setiap jenis memiliki cara perhitungan yang berbeda, tergantung pada posisi dan arah gaya-gaya yang bekerja.
1. Resultan Gaya Searah
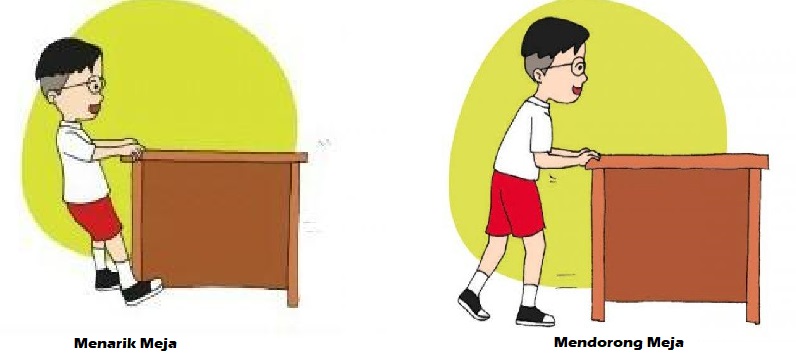
Resultan gaya searah terjadi ketika dua atau lebih gaya bekerja pada benda dalam arah yang sama. Dalam hal ini, resultan gaya dihitung dengan menjumlahkan semua gaya yang bekerja. Contohnya, jika kamu dan adikmu mendorong meja ke arah yang sama, maka resultan gayanya adalah jumlah dari gaya yang kamu berikan dan gaya yang diberikan adikmu.
Rumus umum untuk resultan gaya searah adalah:
$$ F_R = F_1 + F_2 $$
di mana: - $ F_R $ adalah resultan gaya (dalam satuan newton, N) - $ F_1 $ dan $ F_2 $ adalah gaya-gaya yang bekerja dalam arah yang sama
Contoh: Jika kamu mendorong meja dengan gaya 50 N dan adikmu mendorong meja dengan gaya 30 N ke arah yang sama, maka resultan gayanya adalah $ 50 + 30 = 80 $ N.
2. Resultan Gaya Berlawanan Arah
Resultan gaya berlawanan terjadi ketika dua atau lebih gaya bekerja pada benda dalam arah yang berlawanan. Dalam kasus ini, resultan gaya dihitung dengan mengurangkan gaya yang bekerja dalam arah berlawanan. Misalnya, jika kamu mendorong meja ke kanan dengan gaya 50 N dan adikmu mendorong meja ke kiri dengan gaya 40 N, maka resultan gayanya adalah $ 50 - 40 = 10 $ N ke arah kamu.
Rumus umum untuk resultan gaya berlawanan adalah:
$$ F_R = F_1 - F_2 $$
di mana: - $ F_R $ adalah resultan gaya (dalam satuan newton, N) - $ F_1 $ adalah gaya yang bekerja dalam arah tertentu - $ F_2 $ adalah gaya yang bekerja dalam arah berlawanan
Contoh: Jika kamu mendorong meja ke kanan dengan gaya 60 N dan adikmu mendorong meja ke kiri dengan gaya 30 N, maka resultan gayanya adalah $ 60 - 30 = 30 $ N ke arah kamu.
3. Resultan Gaya Tegak Lurus
Resultan gaya tegak lurus terjadi ketika dua gaya bekerja pada benda dalam arah yang saling tegak lurus, seperti horizontal dan vertikal. Dalam kasus ini, resultan gaya dihitung menggunakan teorema Pythagoras karena gaya-gaya tersebut membentuk segitiga siku-siku.
Rumus umum untuk resultan gaya tegak lurus adalah:
$$ F_R = \sqrt{F_1^2 + F_2^2} $$
di mana: - $ F_R $ adalah resultan gaya (dalam satuan newton, N) - $ F_1 $ dan $ F_2 $ adalah gaya-gaya yang bekerja dalam arah tegak lurus
Contoh: Jika kamu mendorong meja ke kanan dengan gaya 30 N dan adikmu mendorong meja ke atas dengan gaya 40 N, maka resultan gayanya adalah $ \sqrt{30^2 + 40^2} = \sqrt{900 + 1600} = \sqrt{2500} = 50 $ N.
Dengan memahami ketiga jenis resultan gaya ini, Anda dapat lebih mudah menyelesaikan berbagai masalah fisika yang melibatkan gaya-gaya yang bekerja pada suatu benda.
Rumus Resultan Gaya yang Membentuk Sudut
Selain tiga jenis resultan gaya yang telah dijelaskan sebelumnya, ada juga kasus khusus di mana gaya-gaya yang bekerja pada suatu benda membentuk sudut tertentu terhadap sumbu-x atau sumbu-y. Dalam situasi ini, kita perlu menguraikan komponen-komponen gaya tersebut agar dapat menghitung resultan gaya secara akurat.
Langkah-Langkah Menghitung Resultan Gaya yang Membentuk Sudut
- Uraikan Komponen Gaya:
Untuk gaya yang membentuk sudut, kita perlu membagi gaya tersebut menjadi komponen-komponen yang sejajar dengan sumbu-x dan sumbu-y. - Komponen gaya pada sumbu-x: $ F_x = F \cdot \cos(\theta) $
-
Komponen gaya pada sumbu-y: $ F_y = F \cdot \sin(\theta) $
-
Hitung Resultan Gaya pada Setiap Sumbu:
Setelah komponen gaya diketahui, kita dapat menghitung resultan gaya pada sumbu-x dan sumbu-y. - Resultan gaya pada sumbu-x: $ \sum F_x = F_{1x} + F_{2x} $
-
Resultan gaya pada sumbu-y: $ \sum F_y = F_{1y} + F_{2y} $
-
Hitung Resultan Gaya Total:
Setelah mengetahui resultan gaya pada sumbu-x dan sumbu-y, kita dapat menghitung resultan gaya total menggunakan teorema Pythagoras.
$$ F_R = \sqrt{(\sum F_x)^2 + (\sum F_y)^2} $$
Contoh Soal
Sebuah benda dikenai dua gaya:
- Gaya pertama ($ F_1 $) sebesar 10 N dengan sudut $ 30^\circ $ terhadap sumbu-x.
- Gaya kedua ($ F_2 $) sebesar 15 N dengan sudut $ 60^\circ $ terhadap sumbu-x.
Langkah-langkah Penyelesaian:
1. Uraikan komponen gaya:
- $ F_{1x} = 10 \cdot \cos(30^\circ) = 10 \cdot \frac{\sqrt{3}}{2} = 8.66 $ N
- $ F_{1y} = 10 \cdot \sin(30^\circ) = 10 \cdot \frac{1}{2} = 5 $ N
- $ F_{2x} = 15 \cdot \cos(60^\circ) = 15 \cdot \frac{1}{2} = 7.5 $ N
- $ F_{2y} = 15 \cdot \sin(60^\circ) = 15 \cdot \frac{\sqrt{3}}{2} = 12.99 $ N
- Hitung resultan gaya pada setiap sumbu:
- $ \sum F_x = 8.66 + 7.5 = 16.16 $ N
-
$ \sum F_y = 5 + 12.99 = 17.99 $ N
-
Hitung resultan gaya total:
$$ F_R = \sqrt{(16.16)^2 + (17.99)^2} = \sqrt{261.14 + 323.64} = \sqrt{584.78} \approx 24.18 \text{ N} $$
Dengan demikian, resultan gaya totalnya adalah sekitar 24.18 N. Ini menunjukkan bahwa gaya-gaya yang bekerja pada benda tersebut menghasilkan resultan gaya yang cukup besar, meskipun masing-masing gaya memiliki sudut yang berbeda.
Penerapan Resultan Gaya dalam Kehidupan Sehari-Hari
Resultan gaya tidak hanya relevan dalam konteks fisika teoritis, tetapi juga memiliki penerapan praktis dalam kehidupan sehari-hari. Beberapa contoh penerapan resultan gaya yang umum dapat ditemukan dalam berbagai aktivitas dan situasi, seperti:
1. Permainan Tarik Tambang
Permainan tarik tambang adalah contoh nyata dari penerapan resultan gaya. Saat dua tim saling menarik tambang, resultan gaya menentukan kemenangan tim yang memiliki gaya tarik yang lebih besar. Misalnya, jika tim A menarik tambang dengan gaya 50 N dan tim B dengan gaya 40 N, maka resultan gaya akan mengarah ke tim A, sehingga tim A menang.
2. Perahu Dayung
Dalam perahu dayung, resultan gaya berperan penting dalam gerakan perahu. Ketika dayung ditarik ke belakang, perahu akan bergerak ke depan karena adanya gaya aksi dan reaksi. Resultan gaya yang bekerja pada perahu adalah kombinasi dari gaya dorong dayung dan gaya gesek air. Jika gaya dorong lebih besar dari gaya gesek, maka perahu akan bergerak.
3. Mendayung Perahu
Saat mendayung perahu, gaya yang diberikan oleh dayung harus menghasilkan resultan gaya yang cukup besar untuk mengatasi gaya gesek air. Jika dayung ditarik dengan gaya yang tepat, maka perahu akan bergerak maju. Jika gaya yang diberikan terlalu kecil, maka perahu tidak akan bergerak.
4. Menarik Benda
Ketika seseorang menarik benda, seperti kotak atau meja, resultan gaya menentukan apakah benda tersebut akan bergerak atau tetap diam. Jika gaya tarik yang diberikan lebih besar dari gaya gesek, maka benda akan bergerak. Jika gaya tarik sama dengan gaya gesek, maka benda akan tetap diam.
5. Gerakan Mobil
Ketika mobil bergerak, resultan gaya antara gaya mesin dan gaya gesek jalan menentukan kecepatan dan percepatan mobil. Jika gaya mesin lebih besar dari gaya gesek, maka mobil akan bergerak. Jika gaya gesek lebih besar, maka mobil akan melambat atau berhenti.
Dengan memahami penerapan resultan gaya dalam kehidupan sehari-hari, kita dapat lebih mudah memahami bagaimana gaya bekerja dan bagaimana kita dapat memanfaatkannya dalam berbagai situasi.
Contoh Soal dan Pembahasan
Untuk memperkuat pemahaman tentang rumus resultan gaya, berikut ini beberapa contoh soal yang disertai dengan pembahasan lengkap.
Contoh Soal 1
Haris mendorong meja ke timur dengan gaya 50 N. Tiba-tiba, Tomi datang membantu Haris mendorong meja tersebut ke timur dengan gaya 30 N. Saat Haris dan Tomi asyik mendorong meja ke timur, Robi datang dan mendorong mejanya ke barat dengan gaya 80 N. Menurutmu, apa yang akan terjadi pada meja?
Pembahasan:
- Gaya ke timur: $ F_1 = 50 \, \text{N} $
- Gaya ke timur: $ F_2 = 30 \, \text{N} $
- Gaya ke barat: $ F_3 = 80 \, \text{N} $
Resultan gaya dihitung sebagai berikut:
$$
F_R = F_1 + F_2 - F_3 = 50 + 30 - 80 = 0 \, \text{N}
$$
Karena resultan gaya bernilai nol, meja akan tetap diam.
Contoh Soal 2
Tiga buah gaya bekerja seperti pada gambar berikut. Berapakah resultan gayanya?
Pembahasan:
Misalkan gaya-gaya tersebut adalah:
- $ F_1 = 5 \, \text{N} $ (arah horizontal)
- $ F_2 = 10 \, \text{N} $ (arah vertikal)
- $ F_3 = 10 \, \text{N} $ (arah horizontal, berlawanan dengan $ F_1 $)
Komponen gaya pada sumbu-x:
$$
\sum F_x = F_1 - F_3 = 5 - 10 = -5 \, \text{N}
$$
Komponen gaya pada sumbu-y:
$$
\sum F_y = F_2 = 10 \, \text{N}
$$
Resultan gaya total:
$$
F_R = \sqrt{(-5)^2 + (10)^2} = \sqrt{25 + 100} = \sqrt{125} = 5\sqrt{5} \, \text{N}
$$
Contoh Soal 3
Sebuah kotak bermassa 20 kg dikenai gaya seperti gambar berikut. Berapakah usaha untuk memindahkan kotak tersebut?
Diketahui:
- $ F_1 = 25 \, \text{N} $
- $ F_2 = 40 \, \text{N} $
- $ \theta = 60^\circ $
- $ s = 50 \, \text{cm} = 0,5 \, \text{m} $
Jawaban:
Resultan gaya:
$$
F_R = F_1 + F_2 \cdot \cos(60^\circ) = 25 + (40 \cdot 0,5) = 25 + 20 = 45 \, \text{N}
$$
Usaha:
$$
W = F_R \cdot s = 45 \cdot 0,5 = 22,5 \, \text{Joule}
$$
Dengan demikian, besarnya usaha untuk memindahkan kotak adalah 22,5 J.
Kesimpulan
Resultan gaya adalah konsep penting dalam ilmu fisika yang menjelaskan bagaimana gaya-gaya yang bekerja pada suatu benda saling memengaruhi. Dengan memahami rumus resultan gaya, Anda dapat menghitung resultan gaya yang bekerja pada suatu benda berdasarkan arah dan besar gaya tersebut. Ada tiga jenis utama resultan gaya: searah, berlawanan, dan tegak lurus. Selain itu, terdapat kasus khusus di mana gaya-gaya membentuk sudut tertentu, yang memerlukan penguraian komponen gaya sebelum menghitung resultan.
Penerapan resultan gaya juga sangat luas dalam kehidupan sehari-hari, mulai dari permainan tarik tambang hingga pengangkatan benda. Dengan memahami konsep ini, Anda tidak hanya dapat menyelesaikan soal-soal fisika, tetapi juga memahami bagaimana gaya bekerja di dunia nyata. Semoga artikel ini membantu Anda memahami rumus resultan gaya dengan lebih mudah dan akurat.

0Komentar