Pahami Rumus Transformasi Geometri dengan Mudah dan Lengkap

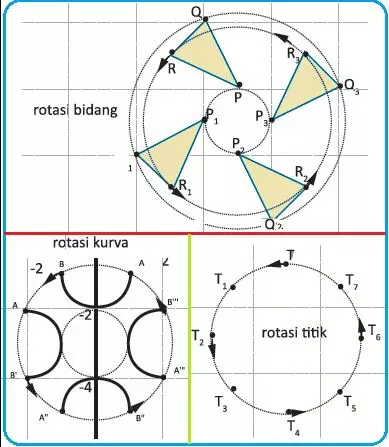
Transformasi geometri adalah konsep penting dalam matematika yang mempelajari perubahan posisi, ukuran, atau bentuk suatu objek di bidang datar. Konsep ini sering digunakan dalam berbagai bidang seperti seni, teknik, dan ilmu komputer. Dengan memahami rumus transformasi geometri, kamu akan lebih mudah menggambarkan dan menganalisis perubahan pada objek geometris. Transformasi geometri terdiri dari empat jenis utama: translasi (pergeseran), refleksi (pencerminan), rotasi (perputaran), dan dilatasi (pembesaran atau pengecilan). Setiap jenis transformasi memiliki rumus dan sifat khusus yang harus dipahami agar dapat diterapkan secara tepat.

Dalam kehidupan sehari-hari, transformasi geometri juga sering muncul, misalnya saat kamu bercermin, melihat bayangan di air, atau bahkan saat bermain game yang menggunakan animasi. Dengan memahami rumus transformasi geometri, kamu tidak hanya bisa menyelesaikan soal-soal matematika tetapi juga mengenali pola-pola yang ada di lingkungan sekitar.

Artikel ini akan membahas secara lengkap setiap jenis transformasi geometri beserta contoh penggunaannya. Kami juga akan memberikan tips dan trik untuk memahami konsep ini dengan lebih mudah. Jadi, jika kamu ingin memahami rumus transformasi geometri secara mendalam, lanjutkan membaca artikel ini hingga selesai!

Pengertian Transformasi Geometri

Transformasi geometri merujuk pada perubahan posisi, ukuran, atau bentuk suatu objek di bidang geometri. Dalam matematika, transformasi ini biasanya dinyatakan dalam bentuk koordinat Cartesius atau matriks. Tujuan dari transformasi geometri adalah untuk memindahkan, memutar, mencerminkan, atau mengubah ukuran suatu objek tanpa menghilangkan karakteristik dasarnya.

Beberapa contoh transformasi geometri yang sering kita temui dalam kehidupan sehari-hari antara lain:

• Translasi: Perpindahan objek dari satu tempat ke tempat lain tanpa mengubah bentuk atau ukurannya.
• Refleksi: Pembentukan bayangan suatu objek sebagai hasil pemantulan terhadap garis tertentu, seperti cermin.
• Rotasi: Perputaran objek sekeliling titik tertentu dengan sudut tertentu.
• Dilatasi: Perubahan ukuran objek baik diperbesar maupun diperkecil, tetapi tidak mengubah bentuknya.

Setiap jenis transformasi memiliki rumus dan cara kerja masing-masing. Dengan memahami rumus-rumus tersebut, kamu akan lebih mudah mengidentifikasi dan menerapkan transformasi dalam berbagai situasi.

Jenis-Jenis Transformasi Geometri

1. Translasi (Pergeseran)

Translasi adalah perpindahan suatu objek dari satu posisi ke posisi lain tanpa mengubah bentuk atau ukurannya. Misalnya, jika sebuah titik $A(x, y)$ ditranslasi sejauh $T(a, b)$, maka titik baru setelah translasi adalah $A'(x + a, y + b)$.

Rumus Umum Translasi: $$ \begin{pmatrix} x' \ y' \end{pmatrix} = \begin{pmatrix} a \ b \end{pmatrix} + \begin{pmatrix} x \ y \end{pmatrix} $$

Contoh: Jika titik $A(2, 3)$ ditranslasi sejauh $(4, -1)$, maka koordinat titik akhirnya adalah: $$ x' = 2 + 4 = 6 \ y' = 3 + (-1) = 2 $$ Sehingga, titik $A'$ adalah $(6, 2)$.

2. Refleksi (Pencerminan)

Refleksi adalah proses pembentukan bayangan suatu objek sebagai hasil pemantulan terhadap garis tertentu. Garis tersebut bisa berupa sumbu-x, sumbu-y, atau garis lain seperti $y = x$ atau $y = -x$.

Rumus Umum Refleksi: - Refleksi terhadap sumbu-x: $$ P'(x, -y) $$ - Refleksi terhadap sumbu-y: $$ P'(-x, y) $$ - Refleksi terhadap garis $y = x$: $$ P'(y, x) $$ - Refleksi terhadap garis $y = -x$: $$ P'(-y, -x) $$

Contoh: Jika titik $B(3, 5)$ direfleksikan terhadap sumbu-x, maka koordinat titik akhirnya adalah: $$ x' = 3 \ y' = -5 $$ Sehingga, titik $B'$ adalah $(3, -5)$.

3. Rotasi (Perputaran)

Rotasi adalah perputaran suatu objek sekeliling titik tertentu dengan sudut tertentu. Sudut rotasi bisa positif (berlawanan arah jarum jam) atau negatif (searah jarum jam).

Rumus Umum Rotasi: Untuk rotasi dengan pusat $(0, 0)$ dan sudut $\alpha$, rumusnya adalah: $$ \begin{pmatrix} x' \ y' \end{pmatrix} = \begin{pmatrix} \cos \alpha & -\sin \alpha \ \sin \alpha & \cos \alpha \end{pmatrix} \begin{pmatrix} x \ y \end{pmatrix} $$

Contoh: Jika titik $C(2, 1)$ dirotasikan sejauh $90^\circ$ berlawanan arah jarum jam terhadap titik asal, maka: $$ \cos 90^\circ = 0, \quad \sin 90^\circ = 1 $$ $$ x' = 0 \cdot 2 - 1 \cdot 1 = -1 \ y' = 1 \cdot 2 + 0 \cdot 1 = 2 $$ Sehingga, titik $C'$ adalah $(-1, 2)$.

4. Dilatasi (Pembesaran/Pengecilan)

Dilatasi adalah proses perubahan ukuran suatu objek, baik diperbesar maupun diperkecil, tanpa mengubah bentuknya. Faktor pengali $k$ menentukan apakah objek diperbesar ($k > 1$) atau diperkecil ($0 < k < 1$).

Rumus Umum Dilatasi: Untuk dilatasi dengan pusat $(0, 0)$ dan faktor $k$, rumusnya adalah: $$ \begin{pmatrix} x' \ y' \end{pmatrix} = \begin{pmatrix} k & 0 \ 0 & k \end{pmatrix} \begin{pmatrix} x \ y \end{pmatrix} $$

Contoh: Jika titik $D(1, 2)$ didilatasi dengan faktor $k = 3$, maka: $$ x' = 3 \cdot 1 = 3 \ y' = 3 \cdot 2 = 6 $$ Sehingga, titik $D'$ adalah $(3, 6)$.

Contoh Soal dan Pembahasan

Soal 1: Translasi

Titik $E(4, 7)$ ditranslasi sejauh $T(3, -2)$. Tentukan koordinat titik akhirnya.

Pembahasan: $$ x' = 4 + 3 = 7 \ y' = 7 + (-2) = 5 $$ Jadi, titik $E'$ adalah $(7, 5)$.

Soal 2: Refleksi

Titik $F(-2, 5)$ direfleksikan terhadap garis $y = x$. Tentukan koordinat titik akhirnya.

Pembahasan: $$ x' = 5 \ y' = -2 $$ Jadi, titik $F'$ adalah $(5, -2)$.

Soal 3: Rotasi

Titik $G(3, -1)$ dirotasikan sejauh $180^\circ$ terhadap titik asal. Tentukan koordinat titik akhirnya.

Pembahasan: $$ \cos 180^\circ = -1, \quad \sin 180^\circ = 0 $$ $$ x' = -1 \cdot 3 - 0 \cdot (-1) = -3 \ y' = 0 \cdot 3 + (-1) \cdot (-1) = 1 $$ Jadi, titik $G'$ adalah $(-3, 1)$.

Soal 4: Dilatasi

Titik $H(2, -4)$ didilatasi dengan faktor $k = -2$ terhadap titik asal. Tentukan koordinat titik akhirnya.

Pembahasan: $$ x' = -2 \cdot 2 = -4 \ y' = -2 \cdot (-4) = 8 $$ Jadi, titik $H'$ adalah $(-4, 8)$.

Tips Menggunakan Rumus Transformasi Geometri

1. Gunakan Gambar: Membuat sketsa sederhana bisa membantu kamu memahami bagaimana objek berubah setelah diterapkan transformasi.
2. Ingat Pola: Setiap jenis transformasi memiliki pola matriks atau rumus yang konsisten. Pelajari pola ini agar lebih mudah mengingat.
3. Latihan Soal: Semakin banyak latihan, semakin mudah kamu menguasai konsep transformasi geometri.
4. Gunakan Warna: Saat mencatat, gunakan warna berbeda untuk setiap jenis transformasi agar lebih menarik dan mudah dipahami.

Kegunaan Transformasi Geometri dalam Kehidupan Sehari-Hari

Transformasi geometri tidak hanya digunakan dalam matematika, tetapi juga dalam berbagai bidang nyata. Berikut beberapa contohnya:

• Animasi: Gerakan karakter dalam film atau game sering menggunakan translasi, rotasi, dan dilatasi.
• Arsitektur: Desain pola ubin atau dinding sering kali melibatkan refleksi dan translasi.
• Robotika: Pergerakan lengan robot sering melibatkan rotasi dan translasi.
• Transportasi: Sistem navigasi GPS menggunakan transformasi geometri untuk memetakan lokasi kendaraan.
• Desain Grafis: Aplikasi seperti Photoshop atau CorelDRAW menggunakan transformasi geometri untuk memutar, memperbesar, atau mencerminkan objek desain.
• Astronomi: Transformasi digunakan untuk memodelkan rotasi bumi dan gerakan bintang di langit malam.

Dengan memahami transformasi geometri, kamu tidak hanya bisa menyelesaikan soal-soal matematika tetapi juga mengenali konsep-konsep yang mendasari berbagai fenomena di dunia nyata. Mulailah belajar dengan latihan soal dan terapkan konsep ini dalam kehidupan sehari-hari untuk meningkatkan pemahamanmu.