Pertidaksamaan linear dua variabel adalah salah satu konsep penting dalam matematika yang sering digunakan untuk menyelesaikan berbagai masalah nyata. Konsep ini memungkinkan kita untuk menggambarkan hubungan antara dua variabel dengan tanda ketidaksamaan seperti <, >, ≤, atau ≥. Dalam kehidupan sehari-hari, pertidaksamaan linear dua variabel dapat diterapkan dalam berbagai situasi, seperti pengelolaan anggaran, perencanaan produksi, atau bahkan dalam bidang ekonomi dan bisnis.
Pertidaksamaan linear dua variabel memiliki bentuk umum ax + by ≤ c, ax + by ≥ c, ax + by < c, atau ax + by > c. Di sini, a dan b adalah koefisien dari variabel x dan y, sedangkan c adalah konstanta. Tujuan utama dari pertidaksamaan linear dua variabel adalah untuk menentukan daerah penyelesaian yang memenuhi kondisi tersebut. Daerah penyelesaian ini biasanya digambarkan dalam sistem koordinat kartesius, di mana garis pembatas membagi bidang menjadi dua bagian, dan salah satu bagian tersebut merupakan solusi dari pertidaksamaan.
Untuk menemukan daerah penyelesaian, ada beberapa metode yang bisa digunakan. Salah satunya adalah metode uji titik, di mana kita memilih titik tertentu di luar garis pembatas dan memasukkan nilai titik tersebut ke dalam pertidaksamaan untuk menentukan apakah titik tersebut termasuk dalam daerah penyelesaian atau tidak. Selain itu, kita juga bisa menggunakan aturan tanda ketidaksamaan untuk menentukan posisi daerah penyelesaian relatif terhadap garis pembatas.
Selain itu, sistem pertidaksamaan linear dua variabel (SPtLDV) juga menjadi topik penting dalam studi ini. SPtLDV terdiri dari dua atau lebih pertidaksamaan linear dua variabel yang harus dipenuhi secara bersamaan. Untuk menyelesaikan SPtLDV, kita perlu menggambar semua garis pembatas dan mencari irisan daerah penyelesaian dari setiap pertidaksamaan.
Dengan memahami konsep dan metode penyelesaian pertidaksamaan linear dua variabel, kita dapat menerapkannya dalam berbagai situasi nyata untuk membuat keputusan yang lebih baik dan efektif. Artikel ini akan membahas secara mendalam tentang pengertian, contoh soal, dan langkah-langkah penyelesaian dari pertidaksamaan linear dua variabel, serta memberikan wawasan tentang penerapan praktisnya dalam kehidupan sehari-hari.
Pengertian Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel adalah suatu bentuk matematika yang mengandung dua variabel (biasanya x dan y) dan tanda ketidaksamaan seperti <, >, ≤, atau ≥. Bentuk umum dari pertidaksamaan linear dua variabel adalah:
- $ ax + by \leq c $
- $ ax + by \geq c $
- $ ax + by < c $
- $ ax + by > c $
Di sini, $ a $ dan $ b $ adalah koefisien dari variabel $ x $ dan $ y $, sedangkan $ c $ adalah konstanta. Tanda ketidaksamaan menunjukkan hubungan antara kedua variabel tersebut. Contohnya, jika kita memiliki pertidaksamaan $ 2x + 3y \leq 6 $, maka kita mencari semua pasangan $ (x, y) $ yang memenuhi kondisi tersebut.
Pertidaksamaan linear dua variabel berbeda dari persamaan linear dua variabel karena persamaan linear dua variabel hanya memiliki satu solusi (sebuah titik), sedangkan pertidaksamaan linear dua variabel memiliki banyak solusi yang membentuk daerah penyelesaian. Daerah penyelesaian ini biasanya digambarkan dalam sistem koordinat kartesius, di mana garis pembatas membagi bidang menjadi dua bagian, dan salah satu bagian tersebut merupakan solusi dari pertidaksamaan.
Bentuk Umum Pertidaksamaan Linear Dua Variabel
Bentuk umum dari pertidaksamaan linear dua variabel adalah sebagai berikut:
- $ ax + by \leq c $
- $ ax + by \geq c $
- $ ax + by < c $
- $ ax + by > c $
Di sini: - $ a $ dan $ b $ adalah koefisien dari variabel $ x $ dan $ y $. - $ c $ adalah konstanta. - $ x $ dan $ y $ adalah variabel yang ingin kita cari solusinya.
Contoh dari bentuk-bentuk ini adalah: - $ 3x + 4y \leq 12 $ - $ 5x - 2y \geq 10 $ - $ -x + 3y < 6 $ - $ 2x + 7y > 14 $
Setiap bentuk ini memiliki cara penyelesaian yang mirip, tetapi hasil akhirnya berbeda tergantung pada tanda ketidaksamaan yang digunakan. Misalnya, jika tanda ketidaksamaan adalah $ \leq $ atau $ \geq $, garis pembatas digambar penuh, sedangkan jika tanda ketidaksamaan adalah $ < $ atau $ > $, garis pembatas digambar putus-putus.
Metode Penyelesaian Pertidaksamaan Linear Dua Variabel
Ada beberapa metode yang dapat digunakan untuk menyelesaikan pertidaksamaan linear dua variabel. Berikut ini adalah beberapa metode yang umum digunakan:
1. Metode Uji Titik
Metode uji titik melibatkan pemilihan sebuah titik di luar garis pembatas dan memasukkan nilai titik tersebut ke dalam pertidaksamaan untuk menentukan apakah titik tersebut termasuk dalam daerah penyelesaian atau tidak. Langkah-langkahnya adalah sebagai berikut: 1. Gambarlah grafik $ ax + by = c $. 2. Jika tanda ketidaksamaan berupa $ \leq $ atau $ \geq $, garis pembatas digambar penuh. Jika tanda ketidaksamaan berupa $ < $ atau $ > $, garis pembatas digambar putus-putus. 3. Ambil sembarang titik, misalnya $ (x_1, y_1) $, di luar garis $ ax + by = c $. 4. Masukkan nilai titik $ (x_1, y_1) $ ke dalam pertidaksamaan $ ax + by \leq c $. 5. Jika hasilnya benar, daerah penyelesaiannya adalah daerah yang memuat titik $ (x_1, y_1) $. Jika hasilnya salah, daerah penyelesaiannya adalah daerah yang tidak memuat titik $ (x_1, y_1) $.
2. Memperhatikan Tanda Ketidaksamaan
Tanda ketidaksamaan juga dapat digunakan untuk menentukan posisi daerah penyelesaian relatif terhadap garis pembatas. Berikut ini adalah langkah-langkahnya: 1. Pastikan koefisien $ x $ dari pertidaksamaan linear dua variabel tersebut positif. Jika tidak positif, kalikan pertidaksamaan dengan -1. Ingat, jika pertidaksamaan dikali -1, tanda ketidaksamaan berubah. 2. Jika koefisien $ x $ sudah positif, perhatikan tanda ketidaksamaannya: - Jika tanda ketidaksamaan $ < $, daerah penyelesaian berada di kiri garis pembatas. - Jika tanda ketidaksamaan $ \leq $, daerah penyelesaian ada di kiri dan pada garis pembatas. - Jika tanda ketidaksamaan $ > $, daerah penyelesaian ada di kanan garis pembatas. - Jika tanda ketidaksamaan $ \geq $, daerah penyelesaian ada di kanan dan pada garis pembatas.
3. Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel (SPtLDV) adalah gabungan dari dua atau lebih pertidaksamaan linear dua variabel. Langkah-langkah penyelesaiannya adalah sebagai berikut: 1. Cari titik $ x $ saat $ y = 0 $, begitu juga sebaliknya. 2. Gambarlah grafik sesuai dengan titik $ x $ dan $ y $. 3. Arsir daerah yang sesuai dengan tanda pertidaksamaan.
Dengan menggunakan metode-metode ini, kita dapat menentukan daerah penyelesaian dari pertidaksamaan linear dua variabel dengan lebih mudah dan akurat.
Contoh Soal Pertidaksamaan Linear Dua Variabel
Berikut ini adalah beberapa contoh soal pertidaksamaan linear dua variabel beserta penyelesaiannya:
Contoh Soal 1
Soal: Tentukan daerah penyelesaian dari pertidaksamaan linear dua variabel $ 5x + 6y > 30 $.
Penyelesaian: 1. Mencari nilai $ x $: - Jika $ y = 0 $, maka $ 5x = 30 $ → $ x = 6 $. 2. Mencari nilai $ y $: - Jika $ x = 0 $, maka $ 6y = 30 $ → $ y = 5 $. 3. Gambarlah grafik dengan titik $ x = 6 $ dan $ y = 5 $ atau $ (6, 5) $. 4. Arsir daerah sesuai dengan tanda pertidaksamaan.
Contoh Soal 2
Soal: Diketahui pertidaksamaan linear dua variabel $ -4x + 2y \leq 8 $. Tentukan daerah penyelesaiannya.
Penyelesaian: 1. Kalikan dengan -1, menjadi $ 4x + 2y \geq 8 $. 2. Mencari nilai $ x $: - Jika $ y = 0 $, maka $ 4x = 8 $ → $ x = 2 $. 3. Mencari nilai $ y $: - Jika $ x = 0 $, maka $ 2y = 8 $ → $ y = 4 $. 4. Gambarlah grafik dengan titik $ x = 2 $ dan $ y = 4 $ atau $ (2, 4) $. 5. Arsir daerah sesuai dengan tanda pertidaksamaan.
Contoh Soal 3
Soal: Diketahui pertidaksamaan linear dua variabel $ 8x + 4y \geq 40 $. Tentukan daerah penyelesaiannya.
Penyelesaian: 1. Mencari nilai $ x $: - Jika $ y = 0 $, maka $ 8x = 40 $ → $ x = 5 $. 2. Mencari nilai $ y $: - Jika $ x = 0 $, maka $ 4y = 40 $ → $ y = 10 $. 3. Gambarlah grafik dengan titik $ x = 5 $ dan $ y = 10 $ atau $ (5, 10) $. 4. Arsir daerah sesuai dengan tanda pertidaksamaan.
Contoh Soal 4
Soal: Sistem pertidaksamaan yang memenuhi daerah yang diarsir pada gambar berikut adalah...
Penyelesaian: 1. Titik-titik yang diberikan adalah $ (0,6) $ dan $ (7,0) $. 2. Persamaan garis: $ 6x + 7y = 42 $. 3. Daerah yang diarsir berada di sebelah kiri garis $ 6x + 7y = 42 $, berarti pertidaksamaannya: $ 6x + 7y \leq 42 $. 4. Titik-titik lain yang diberikan adalah $ (0,4) $ dan $ (9,0) $. 5. Persamaan garis: $ 4x + 9y = 36 $. 6. Daerah yang diarsir berada di sebelah kanan, berarti pertidaksamaannya: $ 4x + 7y \geq 36 $. 7. Batasan tambahan: $ x \geq 0 $ dan $ y \geq 0 $. 8. Jadi, sistem pertidaksamaannya adalah $ 6x + 7y \leq 42 $, $ 4x + 7y \geq 36 $, $ x \geq 0 $, $ y \geq 0 $.
Contoh Soal 5
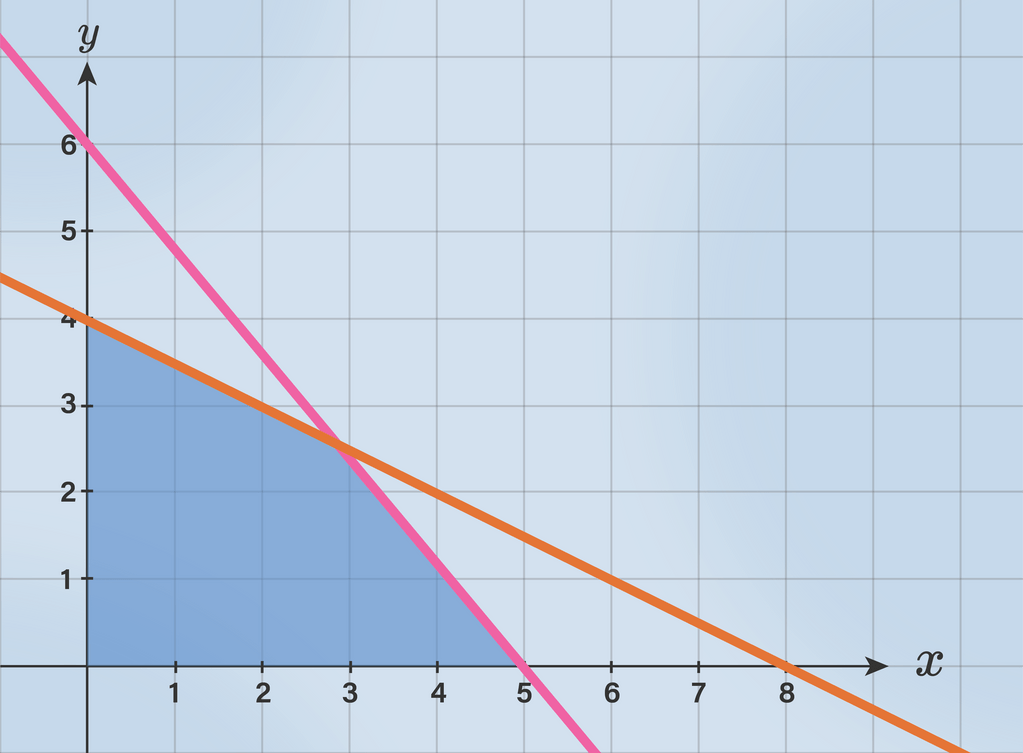
Soal: Buatlah daerah penyelesaian dari pertidaksamaan berikut $ x + y \leq 6 $, $ 2x + 3y \leq 12 $, $ x \geq 1 $, $ y \geq 0 $.
Penyelesaian: 1. Tentukan titik-titik untuk $ x + y \leq 6 $: - $ x + y = 6 $ → titik $ (0,6) $ dan $ (6,0) $. 2. Tentukan titik-titik untuk $ 2x + 3y \leq 12 $: - $ 2x + 3y = 12 $ → titik $ (0,4) $ dan $ (6,0) $. 3. Gambarkan grafik sesuai dengan titik-titik yang ditemukan. 4. Arsir daerah yang sesuai dengan tanda pertidaksamaan.
Dengan mengerjakan contoh soal ini, kita dapat memahami lebih dalam tentang bagaimana menyelesaikan pertidaksamaan linear dua variabel dan menentukan daerah penyelesaiannya.
Penerapan Pertidaksamaan Linear Dua Variabel dalam Kehidupan Nyata
Pertidaksamaan linear dua variabel memiliki banyak penerapan dalam kehidupan nyata, terutama dalam bidang ekonomi, bisnis, dan manajemen. Berikut ini adalah beberapa contoh penerapan pertidaksamaan linear dua variabel dalam situasi nyata:
1. Pengelolaan Anggaran
Misalkan seseorang memiliki anggaran bulanan sebesar Rp 5 juta dan ingin membagi anggaran tersebut antara pengeluaran untuk kebutuhan pokok (x) dan pengeluaran untuk hiburan (y). Pertidaksamaan linear dua variabel yang relevan adalah $ x + y \leq 5000000 $. Dengan menggunakan pertidaksamaan ini, orang tersebut dapat menentukan berapa besar pengeluaran untuk kebutuhan pokok dan hiburan yang dapat dibuat tanpa melebihi anggaran yang tersedia.
2. Perencanaan Produksi
Seorang produsen ingin memproduksi dua jenis produk, A dan B, dengan biaya produksi masing-masing sebesar Rp 100.000 dan Rp 150.000. Jika total biaya produksi tidak boleh melebihi Rp 10 juta, pertidaksamaan linear dua variabel yang relevan adalah $ 100000x + 150000y \leq 10000000 $. Dengan menggunakan pertidaksamaan ini, produsen dapat menentukan jumlah maksimum produk A dan B yang dapat diproduksi tanpa melebihi batas biaya produksi.
3. Manajemen Sumber Daya
Seorang petani ingin menanam dua jenis tanaman, jagung dan padi, dengan luas lahan yang tersedia sebesar 10 hektar. Jika luas lahan yang digunakan untuk jagung (x) dan padi (y) tidak boleh melebihi 10 hektar, pertidaksamaan linear dua variabel yang relevan adalah $ x + y \leq 10 $. Dengan menggunakan pertidaksamaan ini, petani dapat menentukan luas lahan yang digunakan untuk masing-masing tanaman agar tidak melebihi kapasitas lahan yang tersedia.
4. Analisis Investasi
Seorang investor ingin menanamkan dana sebesar Rp 1 miliar dalam dua jenis aset, saham (x) dan obligasi (y). Jika total investasi tidak boleh melebihi Rp 1 miliar, pertidaksamaan linear dua variabel yang relevan adalah $ x + y \leq 1000000000 $. Dengan menggunakan pertidaksamaan ini, investor dapat menentukan berapa besar dana yang dialokasikan untuk masing-masing aset agar tidak melebihi batas investasi yang direncanakan.
5. Perencanaan Keuangan
Seorang siswa ingin menabung untuk membeli alat elektronik seharga Rp 2 juta. Ia menabung x ribu rupiah dari uang saku harian dan y ribu rupiah dari hasil membantu orang tua. Jumlah tabungan yang diinginkan minimal Rp 2 juta, sehingga pertidaksamaan linear dua variabel yang relevan adalah $ x + y \geq 2000 $. Dengan menggunakan pertidaksamaan ini, siswa dapat menentukan berapa besar tabungan yang harus disisihkan dari uang saku dan hasil kerja paruh waktu untuk mencapai target tabungan yang diinginkan.
Dengan memahami penerapan pertidaksamaan linear dua variabel dalam kehidupan nyata, kita dapat lebih mudah menggunakannya dalam situasi-situasi yang kompleks dan memperoleh hasil yang optimal.


0Komentar