Pengertian dan Perbandingan Trigonometri yang Wajib Diketahui

Trigonometri adalah salah satu cabang matematika yang sangat penting dalam memahami hubungan antara sudut dan sisi pada segitiga. Dalam kehidupan sehari-hari, trigonometri digunakan dalam berbagai bidang seperti teknik, arsitektur, navigasi, dan bahkan dalam pengukuran jarak atau tinggi suatu benda. Salah satu konsep inti dalam trigonometri adalah perbandingan trigonometri, yang merupakan dasar untuk menghitung panjang sisi atau besar sudut dalam segitiga siku-siku.

Perbandingan trigonometri terdiri dari enam fungsi utama: sinus (sin), kosinus (cos), tangen (tan), kosekan (csc), sekan (sec), dan kotangen (cot). Setiap fungsi ini memiliki definisi yang spesifik berdasarkan posisi sisi terhadap sudut yang ditinjau. Dengan memahami perbandingan trigonometri, kita dapat menyelesaikan berbagai masalah matematika dengan lebih efisien dan akurat.

Selain itu, perbandingan trigonometri juga memiliki aplikasi praktis dalam kehidupan nyata. Misalnya, dalam bidang teknik, trigonometri digunakan untuk menghitung tinggi bangunan atau lebar sungai. Dalam bidang navigasi, trigonometri membantu menentukan posisi kapal atau pesawat terbang. Oleh karena itu, pemahaman tentang perbandingan trigonometri sangat penting, baik bagi siswa maupun para profesional di berbagai bidang.

Dalam artikel ini, kita akan membahas secara mendalam tentang pengertian perbandingan trigonometri, rumus-rumus dasar, sudut istimewa, serta contoh soal yang bisa membantu memperdalam pemahaman Anda. Selain itu, kita juga akan menjelaskan bagaimana perbandingan trigonometri digunakan dalam kehidupan sehari-hari dan bagaimana konsep-konsep tambahan seperti aturan sinus, aturan cosinus, dan identitas trigonometri dapat diterapkan dalam penyelesaian masalah.

Definisi Perbandingan Trigonometri

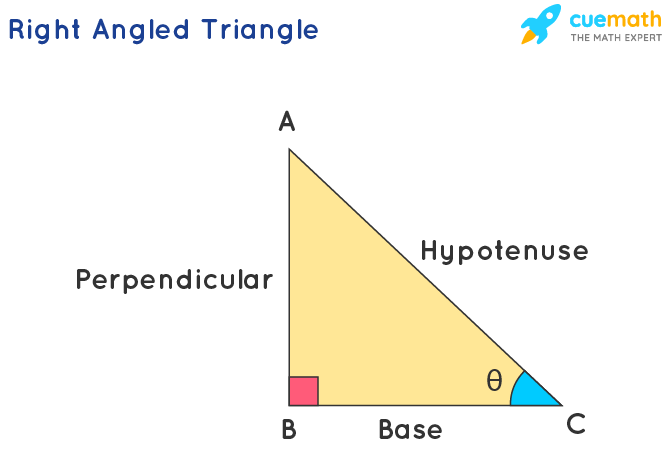
Perbandingan trigonometri adalah rasio antara dua sisi dalam segitiga siku-siku. Segitiga siku-siku memiliki tiga sisi: sisi miring (hipotenusa), sisi depan (sisi yang berhadapan dengan sudut yang ditinjau), dan sisi samping (sisi yang berdekatan dengan sudut yang ditinjau). Berdasarkan posisi sisi tersebut, kita dapat mendefinisikan enam fungsi trigonometri utama:

1. Sinus (sin): Rasio antara sisi depan dan hipotenusa.
2. Kosinus (cos): Rasio antara sisi samping dan hipotenusa.
3. Tangen (tan): Rasio antara sisi depan dan sisi samping.
4. Kosekan (csc): Kebalikan dari sinus, yaitu rasio antara hipotenusa dan sisi depan.
5. Sekan (sec): Kebalikan dari kosinus, yaitu rasio antara hipotenusa dan sisi samping.
6. Kotangen (cot): Kebalikan dari tangen, yaitu rasio antara sisi samping dan sisi depan.

Dengan memahami definisi ini, kita dapat menghitung nilai-nilai trigonometri untuk berbagai sudut dalam segitiga siku-siku. Pemahaman dasar ini menjadi fondasi untuk menyelesaikan masalah trigonometri yang lebih kompleks.

Rumus Dasar Perbandingan Trigonometri

Rumus dasar perbandingan trigonometri adalah sebagai berikut:

• sin(θ) = Sisi Depan / Hipotenusa
• cos(θ) = Sisi Samping / Hipotenusa
• tan(θ) = Sisi Depan / Sisi Samping
• csc(θ) = Hipotenusa / Sisi Depan = 1 / sin(θ)
• sec(θ) = Hipotenusa / Sisi Samping = 1 / cos(θ)
• cot(θ) = Sisi Samping / Sisi Depan = 1 / tan(θ)

Rumus-rumus ini sangat penting dalam menyelesaikan berbagai masalah trigonometri. Pastikan Anda memahami dan menghafal rumus-rumus ini agar dapat menggunakannya dengan mudah dalam berbagai situasi.

Sudut Istimewa dalam Trigonometri

Sudut istimewa adalah sudut-sudut tertentu yang memiliki nilai trigonometri yang mudah diingat, seperti 0°, 30°, 45°, 60°, dan 90°. Nilai trigonometri untuk sudut-sudut ini sering digunakan dalam penyelesaian soal-soal trigonometri tanpa perlu menggunakan kalkulator.

Berikut adalah nilai trigonometri untuk beberapa sudut istimewa:

• 0°:
• sin(0°) = 0
• cos(0°) = 1

• tan(0°) = 0

• 30° (π/6 rad):

• sin(30°) = 1/2
• cos(30°) = √3/2

• tan(30°) = √3/3

• 45° (π/4 rad):

• sin(45°) = √2/2
• cos(45°) = √2/2

• tan(45°) = 1

• 60° (π/3 rad):

• sin(60°) = √3/2
• cos(60°) = 1/2

• tan(60°) = √3

• 90° (π/2 rad):

• sin(90°) = 1
• cos(90°) = 0
• tan(90°) = tidak terdefinisi

Pemahaman tentang sudut istimewa akan mempercepat proses perhitungan dalam soal-soal trigonometri. Dengan menghafal nilai-nilai ini, Anda dapat menyelesaikan banyak soal dengan cepat dan akurat.

Aplikasi Perbandingan Trigonometri dalam Kehidupan Sehari-hari

Perbandingan trigonometri memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Dalam bidang teknik, trigonometri digunakan untuk menghitung tinggi bangunan, lebar sungai, atau jarak antara dua titik yang tidak dapat diukur secara langsung. Dalam bidang navigasi, trigonometri digunakan untuk menentukan posisi kapal atau pesawat terbang. Dalam bidang arsitektur, trigonometri digunakan untuk merancang bangunan dengan sudut yang presisi dan estetis. Bahkan, dalam bidang musik, trigonometri digunakan untuk menganalisis gelombang suara.

Contohnya, dalam pembangunan jembatan, insinyur menggunakan trigonometri untuk menghitung sudut dan panjang balok yang dibutuhkan agar struktur jembatan tetap stabil. Dalam navigasi laut, kapten kapal menggunakan trigonometri untuk menentukan posisi kapal berdasarkan sudut matahari atau bintang. Dalam dunia olahraga, pelompat jauh menggunakan trigonometri untuk menghitung sudut lompatan yang optimal agar mencapai jarak maksimal.

Dengan demikian, perbandingan trigonometri bukan hanya sekadar materi pelajaran matematika, tetapi juga alat yang sangat berguna dalam berbagai bidang kehidupan. Pemahaman tentang konsep ini akan membantu Anda dalam menghadapi berbagai tantangan nyata di dunia sebenarnya.

Rumus Tambahan dalam Trigonometri

Selain rumus dasar, terdapat juga rumus-rumus tambahan dalam trigonometri yang sering digunakan untuk menyelesaikan soal-soal yang lebih kompleks. Beberapa rumus tambahan yang penting antara lain:

Rumus Jumlah dan Selisih Sudut

• sin(A + B) = sin A cos B + cos A sin B
• sin(A – B) = sin A cos B – cos A sin B
• cos(A + B) = cos A cos B – sin A sin B
• cos(A – B) = cos A cos B + sin A sin B
• tan(A + B) = (tan A + tan B) / (1 – tan A tan B)
• tan(A – B) = (tan A – tan B) / (1 + tan A tan B)

Rumus-rumus ini memungkinkan kita untuk menghitung nilai trigonometri dari sudut yang bukan merupakan sudut istimewa, dengan memanfaatkan sudut-sudut istimewa yang lebih mudah dihafal.

Rumus Sudut Ganda

Rumus sudut ganda merupakan kasus khusus dari rumus jumlah sudut, di mana A = B. Rumus sudut ganda sangat berguna untuk menyederhanakan ekspresi trigonometri.

• sin 2A = 2 sin A cos A
• cos 2A = cos² A – sin² A = 2 cos² A – 1 = 1 – 2 sin² A
• tan 2A = 2 tan A / (1 – tan² A)

Rumus Setengah Sudut

Rumus setengah sudut digunakan untuk menghitung nilai trigonometri dari sudut yang merupakan setengah dari sudut yang diketahui.

• sin(A/2) = ± √((1 – cos A) / 2)
• cos(A/2) = ± √((1 + cos A) / 2)
• tan(A/2) = ± √((1 – cos A) / (1 + cos A)) = (1 – cos A) / sin A = sin A / (1 + cos A)

Rumus Perkalian ke Penjumlahan dan Sebaliknya

Rumus ini mengubah perkalian fungsi trigonometri menjadi penjumlahan atau selisih, dan sebaliknya. Ini berguna dalam integrasi dan penyelesaian persamaan trigonometri.

• 2 sin A cos B = sin (A + B) + sin (A – B)
• 2 cos A sin B = sin (A + B) – sin (A – B)
• 2 cos A cos B = cos (A + B) + cos (A – B)
• -2 sin A sin B = cos (A + B) – cos (A – B)

Dengan memahami rumus-rumus tambahan ini, Anda akan lebih siap dalam menghadapi soal-soal trigonometri yang lebih rumit dan kompleks.

Contoh Soal Perbandingan Trigonometri

Untuk memperdalam pemahaman Anda tentang perbandingan trigonometri, mari kita lihat beberapa contoh soal:

Soal 1

Sebuah segitiga siku-siku ABC memiliki sisi AB = 5 cm dan BC = 12 cm. Jika sudut siku-siku berada di A, tentukan nilai sin B, cos B, dan tan B.

Penyelesaian: - Sisi AB = 5 cm (sisi samping) - Sisi BC = 12 cm (sisi depan) - Sisi AC (hipotenusa) dapat dihitung menggunakan teorema Pythagoras: $$ AC = \sqrt{AB^2 + BC^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ cm} $$ - Maka: - $ \sin B = \frac{BC}{AC} = \frac{12}{13} $ - $ \cos B = \frac{AB}{AC} = \frac{5}{13} $ - $ \tan B = \frac{BC}{AB} = \frac{12}{5} $

Soal 2

Jika sin A = 3/5 dan A adalah sudut lancip, tentukan nilai cos A dan tan A.

Penyelesaian: - Diketahui sin A = 3/5, maka sisi depan = 3 dan hipotenusa = 5. - Menggunakan teorema Pythagoras: $$ sisi samping = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 $$ - Maka: - $ \cos A = \frac{4}{5} $ - $ \tan A = \frac{3}{4} $

Dengan mengerjakan contoh soal seperti ini, Anda akan semakin terampil dalam mengaplikasikan rumus-rumus perbandingan trigonometri. Latihan rutin akan membantu meningkatkan kemampuan Anda dalam menyelesaikan berbagai jenis soal trigonometri.

Kesimpulan

Perbandingan trigonometri adalah konsep penting dalam matematika yang memiliki banyak aplikasi dalam kehidupan sehari-hari. Memahami definisi, rumus dasar, sudut istimewa, dan rumus tambahan akan membantu Anda dalam menyelesaikan berbagai masalah trigonometri.

Dengan latihan yang tekun dan pemahaman yang mendalam, Anda akan menguasai perbandingan trigonometri dan dapat menggunakannya untuk memecahkan masalah dalam berbagai bidang ilmu. Perbandingan trigonometri bukan hanya sekadar materi pelajaran, tetapi juga alat yang sangat berguna dalam kehidupan nyata. Dengan memahami konsep ini, Anda akan lebih siap menghadapi tantangan matematika dan masalah nyata di dunia sebenarnya.