Dalam dunia matematika, konsep relasi dan fungsi menjadi salah satu dasar yang sangat penting untuk dipahami. Baik itu dalam pembelajaran di sekolah maupun dalam penerapan nyata di kehidupan sehari-hari. Relasi dan fungsi tidak hanya menjadi bagian dari pelajaran matematika, tetapi juga sering digunakan dalam berbagai bidang seperti ilmu komputer, ekonomi, dan sains. Dengan memahami contoh relasi dan fungsi, siswa akan lebih mudah mengaplikasikan konsep ini dalam penyelesaian soal-soal matematika.
Contoh relasi dan fungsi dapat ditemukan dalam berbagai bentuk, seperti diagram panah, himpunan pasangan berurutan, atau diagram Cartesius. Setiap bentuk tersebut memiliki cara penyajian dan penggunaan yang berbeda, tetapi tujuannya sama yaitu untuk menjelaskan hubungan antara dua himpunan. Dalam konteks pendidikan, contoh relasi dan fungsi sering digunakan sebagai bahan ajar untuk membantu siswa memahami perbedaan antara relasi dan fungsi serta bagaimana keduanya dapat dihitung dan diterapkan dalam berbagai situasi.
Pemahaman tentang contoh relasi dan fungsi juga sangat berguna dalam menyelesaikan berbagai jenis soal matematika. Misalnya, dalam soal-soal yang melibatkan fungsi linear, kuadrat, atau eksponensial, pemahaman tentang relasi dan fungsi akan membantu siswa menentukan nilai variabel yang sesuai dengan aturan fungsi yang diberikan. Selain itu, contoh relasi dan fungsi juga bisa menjadi alat untuk melatih kemampuan logika dan analisis siswa dalam menyelesaikan masalah matematika secara sistematis dan terstruktur.
Memahami Konsep Dasar Relasi dan Fungsi
Relasi dalam matematika merujuk pada hubungan antara elemen-elemen dari dua himpunan. Misalnya, jika kita memiliki himpunan A = {1, 2, 3} dan himpunan B = {a, b, c}, maka relasi antara A dan B bisa berupa pasangan-pasangan seperti (1, a), (2, b), dan (3, c). Dalam hal ini, setiap anggota dari himpunan A dapat memiliki satu atau lebih pasangan dari himpunan B, atau bahkan tidak memiliki pasangan sama sekali.
Sementara itu, fungsi adalah jenis khusus dari relasi. Dalam fungsi, setiap anggota dari himpunan A (daerah asal) harus memiliki tepat satu pasangan di himpunan B (daerah kawan). Ini berarti bahwa tidak ada anggota di himpunan A yang boleh memiliki lebih dari satu pasangan di himpunan B. Jika suatu relasi memenuhi kondisi ini, maka relasi tersebut disebut sebagai fungsi.
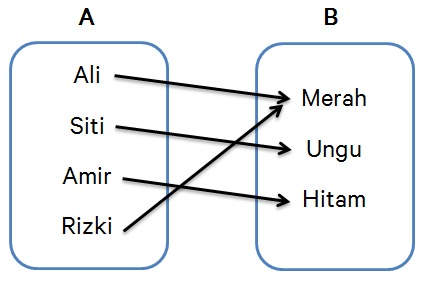
Contoh relasi dan fungsi yang sederhana dapat dilihat dalam bentuk diagram panah. Misalnya, jika himpunan A = {Gita, Wahyu, Tina, Riski} dan himpunan B = {biru, hitam, hijau}, maka relasi antara kedua himpunan tersebut bisa dinyatakan dalam bentuk diagram panah yang menghubungkan setiap nama dengan warna kesukaannya. Jika semua nama memiliki tepat satu warna kesukaan, maka relasi tersebut merupakan fungsi.
Cara Menghitung Relasi dan Fungsi
Untuk menghitung relasi dan fungsi, terdapat beberapa metode yang umum digunakan, seperti diagram panah, himpunan pasangan berurutan, dan diagram Cartesius. Setiap metode memiliki kelebihan dan kekurangan masing-masing, tetapi semuanya bertujuan untuk menjelaskan hubungan antara dua himpunan secara visual atau aljabar.
Diagram Panah: Diagram panah adalah salah satu cara paling sederhana untuk menyajikan relasi. Dalam diagram ini, setiap elemen dari himpunan A diwakili oleh titik atau lingkaran, dan anak panah menghubungkan elemen tersebut ke elemen dari himpunan B yang sesuai. Contoh relasi dan fungsi dalam bentuk diagram panah bisa dilihat pada kasus di mana setiap anggota himpunan A memiliki satu atau lebih pasangan di himpunan B.
Himpunan Pasangan Berurutan: Himpunan pasangan berurutan adalah cara lain untuk menyajikan relasi. Dalam metode ini, setiap pasangan elemen dari himpunan A dan B ditulis dalam bentuk (x, y), di mana x ∈ A dan y ∈ B. Contoh relasi dan fungsi dalam bentuk himpunan pasangan berurutan bisa dilihat pada kasus di mana setiap elemen dari himpunan A dipasangkan dengan satu atau lebih elemen dari himpunan B.
Diagram Cartesius: Diagram Cartesius adalah metode visual yang menggunakan sumbu X dan Y untuk menampilkan hubungan antara dua himpunan. Titik-titik pada diagram ini merepresentasikan pasangan elemen dari himpunan A dan B. Contoh relasi dan fungsi dalam bentuk diagram Cartesius bisa dilihat pada kasus di mana setiap elemen dari himpunan A dipetakan ke satu atau lebih elemen dari himpunan B.
Contoh Soal Relasi dan Fungsi
Untuk memperdalam pemahaman tentang contoh relasi dan fungsi, berikut ini beberapa contoh soal yang bisa dikerjakan:
-
Soal Relasi: Diketahui himpunan A = {1, 2, 3, 4} dan himpunan B = {a, b, c}. Relasi R dari A ke B didefinisikan sebagai R = {(1, a), (2, b), (3, c), (4, a)}. Manakah dari berikut ini yang bukan merupakan pasangan dalam R?
-
a. (2, a)
- b. (4, c)
- c. (1, b)
- d. (3, b)
Jawaban: d. (3, b)
- Soal Fungsi: Diketahui fungsi f(x) = 2x + 2. Hitunglah:
- a. f(5)
- b. Bayangan (-3) oleh f
- c. Nilai f untuk x = 7
- d. Nilai x untuk f(x) = 8
- e. Nilai a jika f(a) = 16
Jawaban: - a. f(5) = 2(5) + 2 = 12 - b. f(-3) = 2(-3) + 2 = -4 - c. f(7) = 2(7) + 2 = 16 - d. f(x) = 8 → 2x + 2 = 8 → x = 3 - e. f(a) = 16 → 2a + 2 = 16 → a = 7
- Soal Fungsi Linear: Diketahui fungsi f(x) = ax + b. Jika f(-1) = 2 dan f(2) = 11, tentukan nilai a dan b.
Jawaban: - f(-1) = -a + b = 2 - f(2) = 2a + b = 11 - Dengan substitusi, diperoleh a = 3 dan b = 5.
Tips Belajar Relasi dan Fungsi
Belajar relasi dan fungsi membutuhkan latihan yang cukup banyak. Berikut beberapa tips yang bisa membantu siswa dalam memahami konsep ini:
- Latihan Soal: Mengerjakan berbagai jenis soal relasi dan fungsi akan membantu siswa memahami berbagai bentuk hubungan antara dua himpunan.
- Visualisasi: Menggunakan diagram panah, himpunan pasangan berurutan, atau diagram Cartesius akan membantu siswa memvisualisasikan hubungan antara elemen-elemen himpunan.
- Pemahaman Konsep Dasar: Memahami perbedaan antara relasi dan fungsi adalah kunci untuk menyelesaikan soal-soal yang berkaitan dengan keduanya.
- Konsistensi: Konsisten dalam belajar dan mempraktikkan konsep relasi dan fungsi akan meningkatkan pemahaman dan kepercayaan diri siswa.
Dengan memahami contoh relasi dan fungsi, siswa akan lebih mudah menghadapi berbagai tantangan dalam matematika dan siap menghadapi ujian atau tes yang melibatkan konsep ini. Pemahaman yang baik tentang relasi dan fungsi juga akan memberikan dasar yang kuat untuk mempelajari materi-materi matematika yang lebih kompleks di masa depan.

0Komentar