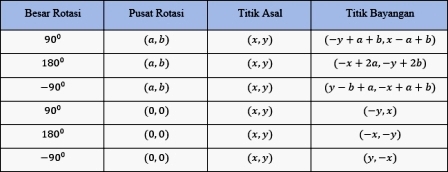
Rotasi dalam matematika adalah salah satu konsep penting dalam transformasi geometri. Dalam kehidupan sehari-hari, kita sering melihat fenomena perputaran, seperti gerakan roda kendaraan atau jarum jam. Di dunia matematika, rotasi digunakan untuk memindahkan titik atau bangun datar pada bidang dengan cara memutar terhadap suatu titik tertentu. Konsep ini sangat berguna dalam berbagai bidang, termasuk fisika, teknik, dan desain grafis.
Rotasi memiliki tiga elemen utama: titik pusat rotasi, besar sudut rotasi, dan arah rotasi. Titik pusat rotasi adalah titik yang menjadi acuan pergerakan putaran. Besar sudut rotasi menunjukkan seberapa besar perputaran dilakukan, sedangkan arah rotasi menentukan apakah perputaran berlawanan atau searah dengan jarum jam.
Pemahaman tentang rotasi tidak hanya membantu dalam menyelesaikan soal-soal matematika, tetapi juga memberikan dasar untuk memahami konsep-konsep lebih lanjut dalam geometri. Dengan mempelajari rotasi, siswa dapat meningkatkan kemampuan mereka dalam menggambar dan menganalisis bentuk-bentuk geometris.
Artikel ini akan membahas secara rinci konsep rotasi, termasuk bagaimana melakukan rotasi terhadap titik pusat (0,0) dan titik pusat (a,b), serta contoh-contoh soal yang dapat membantu memperkuat pemahaman Anda. Mari kita mulai dengan penjelasan dasar tentang rotasi dalam matematika.
Definisi Rotasi dalam Matematika
Rotasi dalam matematika didefinisikan sebagai transformasi yang memindahkan setiap titik pada bidang ke titik lainnya dengan cara memutar pada pusat titik tertentu. Proses ini melibatkan tiga komponen utama: titik pusat rotasi, besar sudut rotasi, dan arah rotasi. Titik pusat rotasi adalah titik yang menjadi acuan pergerakan putaran, sementara besar sudut rotasi menunjukkan seberapa besar perputaran dilakukan. Arah rotasi menentukan apakah perputaran berlawanan atau searah dengan jarum jam.
Dalam matematika, rotasi biasanya dilambangkan dengan notasi $ R(P, \alpha) $, di mana $ P $ adalah pusat rotasi dan $ \alpha $ adalah besar sudut rotasi. Sudut rotasi positif ($ \alpha $) menunjukkan arah putaran berlawanan arah jarum jam, sedangkan sudut rotasi negatif ($ -\alpha $) menunjukkan arah putaran searah jarum jam. Misalnya, jika sebuah titik diputar sebesar $ 90^\circ $ berlawanan arah jarum jam, maka sudut rotasinya adalah $ 90^\circ $. Jika sebaliknya, sudut rotasinya adalah $ -90^\circ $.
Rotasi dapat diterapkan pada berbagai jenis objek, baik titik, garis, maupun bangun datar. Untuk memahami rotasi secara lebih mendalam, kita perlu mempelajari bagaimana melakukan rotasi terhadap titik pusat (0,0) dan titik pusat (a,b). Dengan memahami konsep ini, kita dapat menyelesaikan berbagai soal yang melibatkan rotasi dalam matematika.
Rotasi Terhadap Titik Pusat O(0,0)
Rotasi terhadap titik pusat O(0,0) adalah salah satu bentuk rotasi paling dasar dalam matematika. Dalam rotasi ini, titik awal $ P(x, y) $ akan dirotasikan sejauh sudut $ \theta $ terhadap titik pusat (0,0) dan menghasilkan bayangan $ P'(x', y') $. Secara matematis, rotasi ini dapat dinyatakan dengan persamaan berikut:
$$ \begin{bmatrix} x' \ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} $$
Untuk memahami bagaimana proses ini bekerja, mari kita lihat contoh soal berikut. Misalkan titik $ P(3, 2) $ dirotasikan sejauh $ 135^\circ $ terhadap titik pusat (0,0). Kita dapat menggunakan matriks rotasi untuk menentukan koordinat bayangan titik tersebut. Matriks rotasi untuk $ 135^\circ $ adalah:
$$ \begin{bmatrix} \cos 135^\circ & -\sin 135^\circ \ \sin 135^\circ & \cos 135^\circ \end{bmatrix} = \begin{bmatrix} -\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \ \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix} $$
Dengan mengalikan matriks ini dengan vektor $ \begin{bmatrix} 3 \ 2 \end{bmatrix} $, kita dapat menentukan koordinat bayangan titik $ P' $:
$$ \begin{bmatrix} x' \ y' \end{bmatrix} = \begin{bmatrix} -\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \ \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} 3 \ 2 \end{bmatrix} = \begin{bmatrix} -\frac{5\sqrt{2}}{2} \ \frac{\sqrt{2}}{2} \end{bmatrix} $$
Dengan demikian, koordinat bayangan titik $ P(3, 2) $ setelah dirotasikan sejauh $ 135^\circ $ adalah $ P'\left(-\frac{5\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right) $.
Contoh lain adalah ketika titik $ (4, -3) $ dirotasikan sejauh $ 30^\circ $ terhadap titik pusat (0,0). Matriks rotasi untuk $ 30^\circ $ adalah:
$$ \begin{bmatrix} \cos 30^\circ & -\sin 30^\circ \ \sin 30^\circ & \cos 30^\circ \end{bmatrix} = \begin{bmatrix} \frac{\sqrt{3}}{2} & -\frac{1}{2} \ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} $$
Dengan mengalikan matriks ini dengan vektor $ \begin{bmatrix} 4 \ -3 \end{bmatrix} $, kita dapat menentukan koordinat bayangan titik tersebut:
$$ \begin{bmatrix} x' \ y' \end{bmatrix} = \begin{bmatrix} \frac{\sqrt{3}}{2} & -\frac{1}{2} \ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{bmatrix} \begin{bmatrix} 4 \ -3 \end{bmatrix} = \begin{bmatrix} 2\sqrt{3} + \frac{3}{2} \ 2 - \frac{3}{2}\sqrt{3} \end{bmatrix} $$
Dengan demikian, koordinat bayangan titik $ (4, -3) $ setelah dirotasikan sejauh $ 30^\circ $ adalah $ \left(2\sqrt{3} + \frac{3}{2}, 2 - \frac{3}{2}\sqrt{3}\right) $.
Rotasi Terhadap Titik Pusat (a,b)
Rotasi terhadap titik pusat (a,b) adalah bentuk rotasi yang lebih kompleks karena melibatkan pergeseran titik pusat dari (0,0) ke titik (a,b). Dalam hal ini, titik awal $ P(x, y) $ akan dirotasikan sejauh sudut $ \theta $ terhadap titik pusat (a,b) dan menghasilkan bayangan $ P'(x', y') $. Secara matematis, rotasi ini dapat dinyatakan dengan persamaan berikut:
$$ \begin{bmatrix} x' \ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x-a \ y-b \end{bmatrix} + \begin{bmatrix} a \ b \end{bmatrix} $$
Untuk memahami bagaimana proses ini bekerja, mari kita lihat contoh soal berikut. Misalkan titik $ (2, 4) $ dirotasikan sejauh $ 60^\circ $ searah jarum jam terhadap titik pusat (4,6). Karena arah rotasi searah jarum jam, sudut rotasinya adalah $ -60^\circ $. Matriks rotasi untuk $ -60^\circ $ adalah:
$$ \begin{bmatrix} \cos(-60^\circ) & -\sin(-60^\circ) \ \sin(-60^\circ) & \cos(-60^\circ) \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{\sqrt{3}}{2} \ -\frac{\sqrt{3}}{2} & \frac{1}{2} \end{bmatrix} $$
Dengan mengalikan matriks ini dengan vektor $ \begin{bmatrix} 2-4 \ 4-6 \end{bmatrix} = \begin{bmatrix} -2 \ -2 \end{bmatrix} $, kita dapat menentukan koordinat bayangan titik tersebut:
$$ \begin{bmatrix} x' \ y' \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{\sqrt{3}}{2} \ -\frac{\sqrt{3}}{2} & \frac{1}{2} \end{bmatrix} \begin{bmatrix} -2 \ -2 \end{bmatrix} + \begin{bmatrix} 4 \ 6 \end{bmatrix} = \begin{bmatrix} -1 - \sqrt{3} \ \sqrt{3} - 1 \end{bmatrix} + \begin{bmatrix} 4 \ 6 \end{bmatrix} = \begin{bmatrix} 3 - \sqrt{3} \ 5 + \sqrt{3} \end{bmatrix} $$
Dengan demikian, koordinat bayangan titik $ (2, 4) $ setelah dirotasikan sejauh $ 60^\circ $ searah jarum jam terhadap titik pusat (4,6) adalah $ (3 - \sqrt{3}, 5 + \sqrt{3}) $.
Contoh lain adalah ketika titik $ (2a, -a) $ diputar $ 90^\circ $ berlawanan arah jarum jam dengan pusat perputaran titik $ (1,1) $. Jika hasil rotasi adalah $ (2 + a, -2) $, kita dapat menentukan nilai $ a $ dengan menggunakan persamaan rotasi. Matriks rotasi untuk $ 90^\circ $ adalah:
$$ \begin{bmatrix} \cos 90^\circ & -\sin 90^\circ \ \sin 90^\circ & \cos 90^\circ \end{bmatrix} = \begin{bmatrix} 0 & -1 \ 1 & 0 \end{bmatrix} $$
Dengan mengalikan matriks ini dengan vektor $ \begin{bmatrix} 2a - 1 \ -a - 1 \end{bmatrix} $, kita dapat menentukan koordinat bayangan titik tersebut:
$$ \begin{bmatrix} 2 + a \ -2 \end{bmatrix} = \begin{bmatrix} 0 & -1 \ 1 & 0 \end{bmatrix} \begin{bmatrix} 2a - 1 \ -a - 1 \end{bmatrix} + \begin{bmatrix} 1 \ 1 \end{bmatrix} = \begin{bmatrix} a + 1 \ 2a - 1 \end{bmatrix} + \begin{bmatrix} 1 \ 1 \end{bmatrix} = \begin{bmatrix} a + 2 \ 2a \end{bmatrix} $$
Dengan menyamakan kedua sisi persamaan, kita dapat menentukan bahwa $ 2a = -2 $, sehingga $ a = -1 $.
Contoh Soal Rotasi dalam Matematika
Rotasi dalam matematika sering kali diujikan dalam berbagai bentuk soal, baik itu soal tentang titik, garis, maupun bangun datar. Berikut ini beberapa contoh soal yang dapat membantu memperkuat pemahaman Anda tentang konsep rotasi.
Contoh Soal 1: Rotasi Titik
Misalkan titik $ S(-3, 4) $ dirotasikan sejauh $ 90^\circ $ searah jarum jam terhadap titik pusat (0,0). Tentukan koordinat akhir titik $ S $!
Penyelesaian:
Karena arah rotasi searah jarum jam, sudut rotasinya adalah $ -90^\circ $. Matriks rotasi untuk $ -90^\circ $ adalah:
$$ \begin{bmatrix} \cos(-90^\circ) & -\sin(-90^\circ) \ \sin(-90^\circ) & \cos(-90^\circ) \end{bmatrix} = \begin{bmatrix} 0 & 1 \ -1 & 0 \end{bmatrix} $$
Dengan mengalikan matriks ini dengan vektor $ \begin{bmatrix} -3 \ 4 \end{bmatrix} $, kita dapat menentukan koordinat bayangan titik $ S $:
$$ \begin{bmatrix} x' \ y' \end{bmatrix} = \begin{bmatrix} 0 & 1 \ -1 & 0 \end{bmatrix} \begin{bmatrix} -3 \ 4 \end{bmatrix} = \begin{bmatrix} 4 \ 3 \end{bmatrix} $$
Dengan demikian, koordinat akhir titik $ S $ setelah dirotasikan adalah $ (4, 3) $.
Contoh Soal 2: Rotasi Garis
Misalkan garis $ y = 6x + 2 $ dirotasikan sejauh $ 45^\circ $ terhadap titik pusat (0,0). Tentukan persamaan garis hasil rotasi tersebut!
Penyelesaian:
Matriks rotasi untuk $ 45^\circ $ adalah:
$$ \begin{bmatrix} \cos 45^\circ & -\sin 45^\circ \ \sin 45^\circ & \cos 45^\circ \end{bmatrix} = \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} $$
Dengan mengubah persamaan garis $ y = 6x + 2 $ menjadi bentuk matriks, kita dapat menentukan persamaan garis hasil rotasi. Setelah melakukan perhitungan, kita dapat menemukan bahwa persamaan garis hasil rotasi adalah $ 7\sqrt{2}x + 5\sqrt{2}y + 4 = 0 $.
Contoh Soal 3: Rotasi Bangun Datar
Misalkan segitiga $ KLM $ dengan koordinat titik $ K(-4, 4) $, $ L(-4, 2) $, dan $ M(-2, 2) $ dirotasikan sejauh $ 180^\circ $ terhadap titik pusat (1,2). Tentukan koordinat akhir titik-titik tersebut!
Penyelesaian:
Matriks rotasi untuk $ 180^\circ $ adalah:
$$ \begin{bmatrix} \cos 180^\circ & -\sin 180^\circ \ \sin 180^\circ & \cos 180^\circ \end{bmatrix} = \begin{bmatrix} -1 & 0 \ 0 & -1 \end{bmatrix} $$
Dengan mengalikan matriks ini dengan vektor koordinat titik-titik $ K $, $ L $, dan $ M $, kita dapat menentukan koordinat akhir titik-titik tersebut. Setelah perhitungan, diperoleh koordinat akhir titik $ K(6, 0) $, $ L(6, 2) $, dan $ M(4, 2) $.
Manfaat dan Penerapan Rotasi dalam Kehidupan Sehari-hari
Rotasi dalam matematika tidak hanya berguna dalam menyelesaikan soal-soal geometri, tetapi juga memiliki berbagai penerapan dalam kehidupan sehari-hari. Salah satu contoh penerapan rotasi adalah dalam bidang teknik dan desain grafis, di mana rotasi digunakan untuk memutar objek atau gambar agar sesuai dengan kebutuhan desain. Selain itu, rotasi juga digunakan dalam pengembangan perangkat lunak grafis dan animasi untuk menciptakan efek visual yang menarik.
Dalam bidang fisika, rotasi digunakan untuk menganalisis gerakan benda berputar, seperti roda kendaraan atau bintang yang berotasi. Dengan memahami konsep rotasi, ilmuwan dan insinyur dapat merancang sistem yang lebih efisien dan aman.
Selain itu, rotasi juga digunakan dalam navigasi dan penginderaan jauh. Misalnya, dalam sistem GPS, rotasi digunakan untuk menghitung posisi dan arah perjalanan. Dengan memahami rotasi, kita dapat lebih mudah memahami bagaimana perangkat elektronik bekerja dan mengoptimalkan penggunaannya.
Dalam pendidikan, rotasi menjadi salah satu topik penting dalam mata pelajaran matematika, terutama dalam bab transformasi geometri. Dengan mempelajari rotasi, siswa dapat meningkatkan kemampuan mereka dalam menggambar dan menganalisis bentuk-bentuk geometris. Selain itu, rotasi juga membantu siswa dalam memahami konsep-konsep lain dalam matematika, seperti trigonometri dan vektor.
Dengan demikian, rotasi dalam matematika memiliki manfaat yang luas dan beragam, baik dalam kehidupan sehari-hari maupun dalam berbagai bidang studi. Dengan memahami konsep rotasi, kita dapat lebih mudah memahami dan mengaplikasikan konsep-konsep matematika dalam kehidupan nyata.


0Komentar